Stochastic Gradient Estimation for Higher-order Differentiable Rendering
ICCV 2025
Zican Wang1, Michael Fischer1,2, Tobias Ritschel1
1University College London, 2Adobe Research
We derive methods to compute higher order differentials(Hessians and Hessian-vector products) of the rendering operator. Our approach is based on importance sampling of a convolution that represents the differentials of rendering parameters and shows to be applicable to both rasterization and path tracing. We further suggest an aggregate sampling strategy to importance-sample multiple dimensions of one convolution kernel simultaneously. We demonstrate that this information improves convergence when used in higher-order optimizers such as Newton or Conjugate Gradient relative to a gradient descent baseline in several inverse rendering tasks.

Interactive Demo
Below is an interactive 1D example which uses our higher order method to differentiate through a discontinuous step function. The task here is to move the triangle center (parameterized by theta), such that it covers the grey pixel at the bottom. The plateaus in the cost landscape come from the fact that the error between the pixel's desired color and its current color does not take into account how "far away" the triangle is when it's not overlapping the pixel. We can smoothen these plateaus by our proposed convolution with a Gaussian kernel (displayed in plot in the top left corner, click 'Show Smooth' to see the convolved function). We then sample this convoluted space to estimate a second order gradient (Hessian) and use the samples to drive a second order optimizer(Newton) that moves the initial parameter (blue) towards the region of zero cost, i.e., such that the triangle overlaps the pixel. This is compared to the original first order method that is shown in red.
Derivation
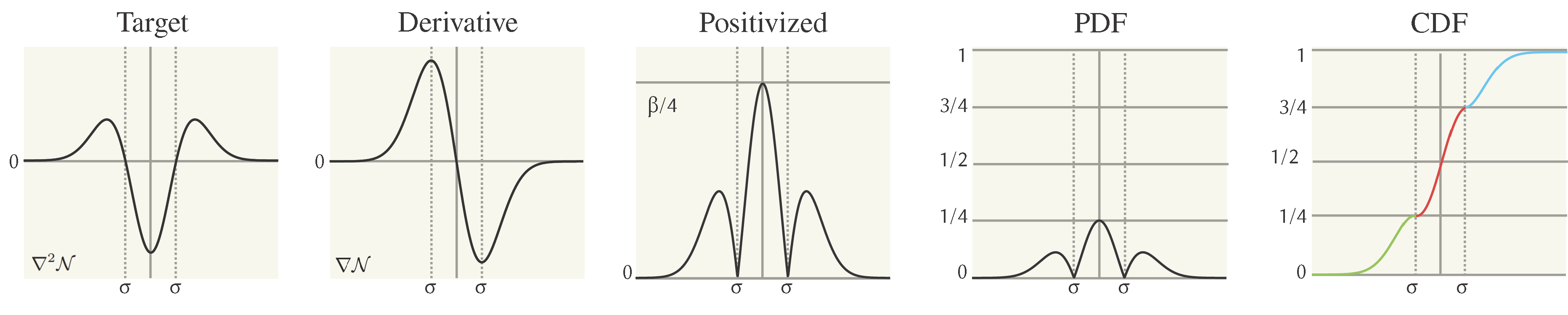
The Hessian of a multivariate Gaussian function describes the second-order partial derivatives of that function. For sampling a diagonal Gaussian Hessian, we can use inverse transform sampling via the Smirnov transform. To allow sampling with this method, the 2nd order derivative is positivized and normalized in to a probability density function. Since the curvature of the Gaussian is the derivative of its gradient, we can get the CDF by scaling and combining the gradient of the Gaussian. For a off-diagonal entry \( H_{ij}(x) \) in the Hessian matrix is given by: \[ H_{ij}(x) = \frac{\partial^2 f}{\partial x_i \partial x_j} \] Because the multivariate Gaussian is separable, each Hessian component decomposes as follows:
- The second derivative of the 1D Gaussian in \(x_i\) and \(x_j\)
- Times the Gaussian (unchanged) in the other dimensions.
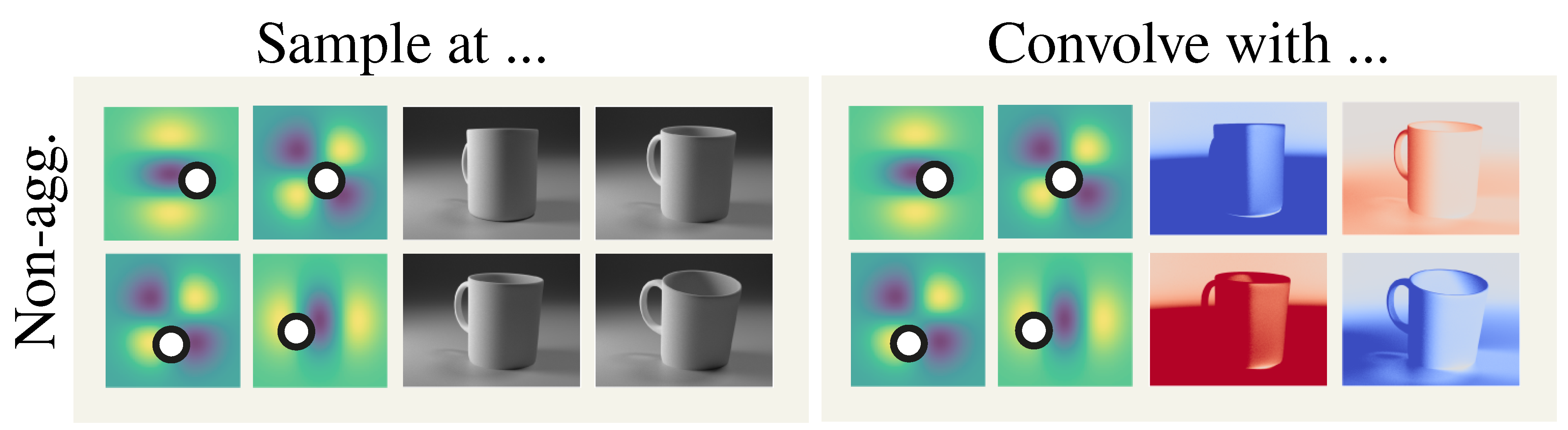
Aggregate sampling
However, the sampling operation would be too costly for Hessians because each dimension need to be sampled individually.
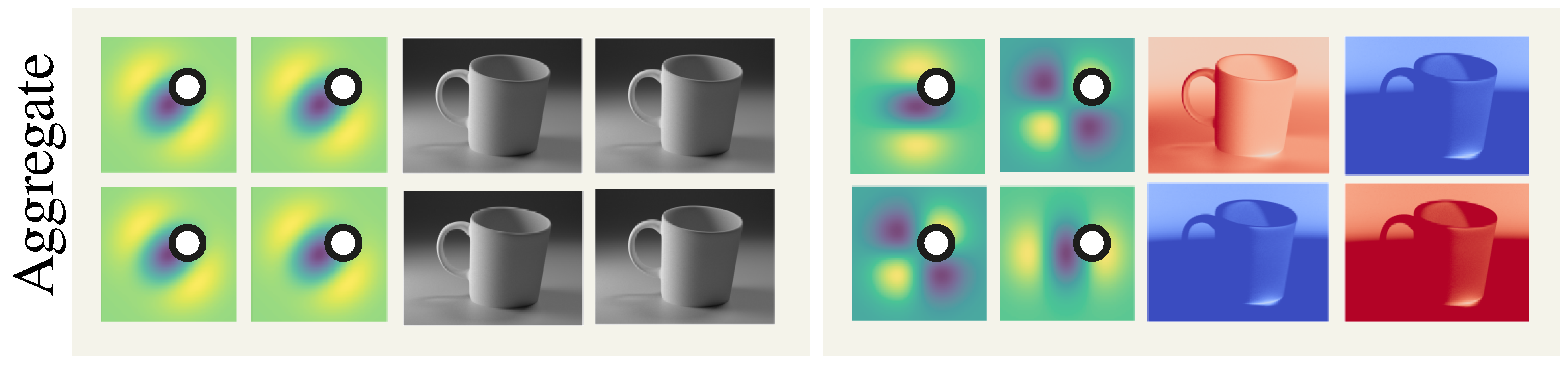
So the average of the PDF for all dimensions is sampled once and convolved with different weights:
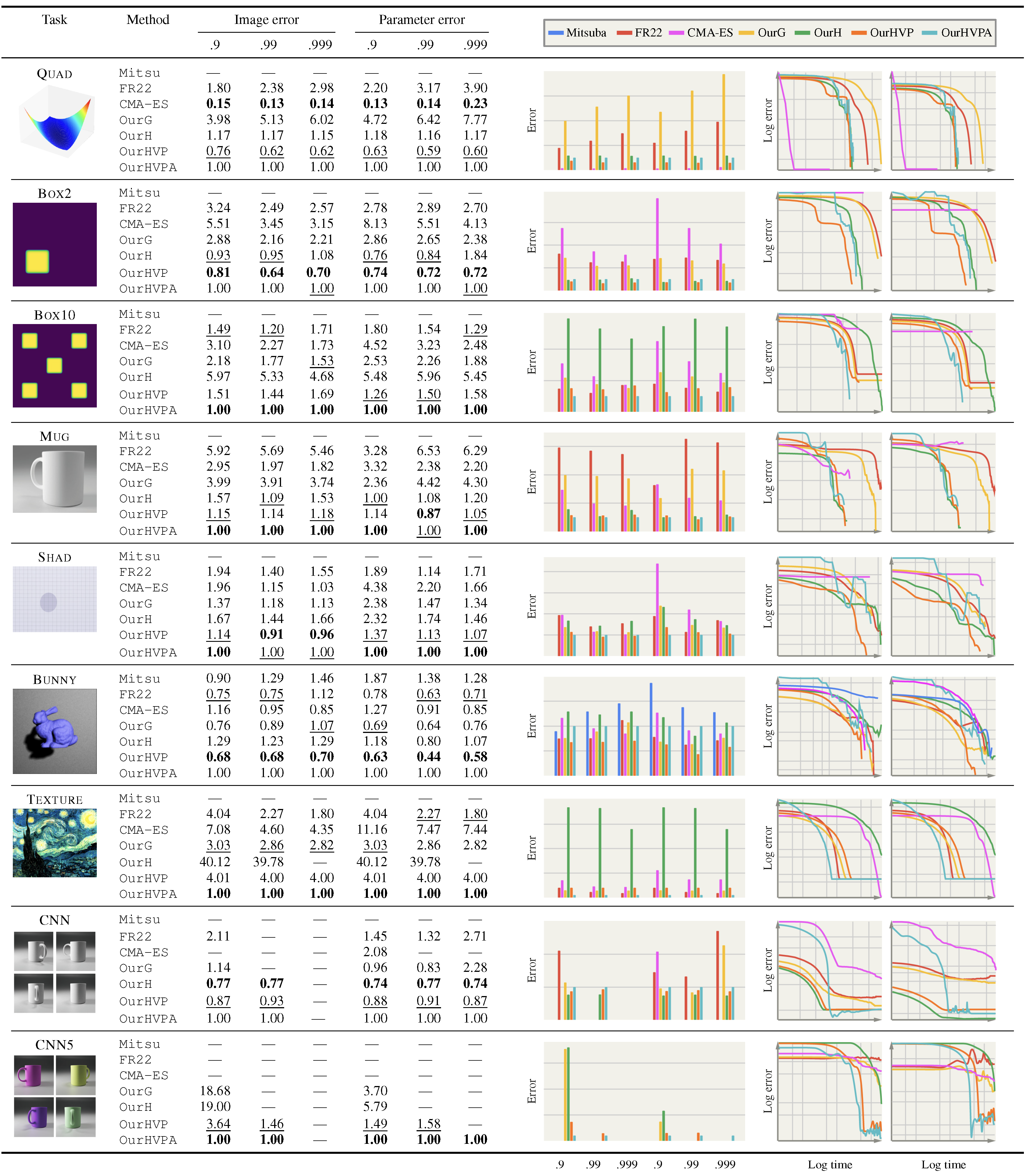
Quantitative results of different methods on different tasks (rows) and their convergence plots. We report convergence time in wall-clock units, in ratio to the overall best method, OurHVPA. In the numerical columns, .9 and .99 report the time taken to achieve 90 and 99% error reduction from the initial starting configuration, respectively, while the bar plots graphically show these findings. The line plots report image- and parameter-space convergence in the left and right column, respectively, on a log-log scale. Methods:
Acknowledgements
Our approach is based on the PRDPT paper by Michael Fischer and Tobias Ritschel. With additional higher order optimization and sampling scheme. Please check out the original paper here.
